La menace quantique
Florian Cloarec, Quentin Trombini
L’entreprise IBM a récemment annoncé qu’elle pourrait commercialiser dès 2023 des ordinateurs quantiques pour le public1. Au même moment, la startup QuEra, fondée par des physiciens de Harvard et du MIT, communiquait sur un nouveau record dans les capacités de calcul quantique, à 256 qubits, bien loin devant les 53 qubits de Google ou IBM2.
Ces successions d’annonces ouvrent-elles une nouvelle époque pour l’informatique quantique ? Quel peut être l’impact de l’explosion des capacités de calcul ? Pourquoi l’informatique quantique n’a-t-elle rien à voir avoir celle que nous connaissons ? Quelles seront les applications ? Comment vont-elles chambouler la manière dont nous transmettons et sécurisons nos données ?
Principes de l'informatique quantique
Tout comme l’informatique dite « classique », l’informatique quantique est composée de 0 et de 1, mais les bits constitués d’électricité sont remplacés par des q-bits qui eux sont constitués de niveaux d’énergie de façon à mobiliser des phénomènes quantiques. Pour ce faire, les puces doivent être refroidies à 0,00014 kelvin, l’équivalent de -273 degrés Celsius. Ainsi, la température intérieure de la machine que vous apercevez sur l’image ci-contre est comprise entre 15 et 0,00014 Kelvin. Cette contrainte est ce qui rend la construction et la commercialisation d’ordinateurs quantiques si difficile. Pourquoi se l’imposer ? Elle permet d’ajouter un état de superposition, qui correspond en même temps à un zéro et un et qui s’écrit (½)(|0›+|1›). Cet état de superposition est créé par l’envoi de micro-ondes sur la puce afin d’exciter son niveau d’énergie pour le mettre entre l’état 0 et l’état 13.
L’existence de ces états de superposition change du tout au tout les manières de conduire le calcul. Cela permet, par exemple, de chercher dans l’intégralité d’une liste en même temps ! Fondamentalement, les calculs d’un ordinateur quantique ne reposent plus sur le même type de calcul de puissance qu’un ordinateur classique. La complexité ne repose plus sur le nombre de passages dans une boucle, mais plutôt sur la complexité de la fonction mathématique de calculs cachée derrière chaque algorithme. Actuellement les algorithmes optimisés pour le calcule quantique sont ceux capables de vérifier si une fonction est continue ou équilibrée. Ainsi que celui permettant de parcourir une liste plus rapidement, l’algorithme de Shor dont nous parlerons plus tard et pour finir la génération de nombres aléatoires.
Les algorithmes cités précédemment sont plus rapides que des algorithmes classiques, mais ne suffisent pas à atteindre ce qu’on appelle la « suprématie quantique ». Cette suprématie quantique correspond au moment où les ordinateurs quantiques seront capables de résoudre un problème qu’un ordinateur « classique » ne serait pas capable de résoudre en un temps correct. Si elle n’a pour l’instant pas été atteinte, IBM et Google affirment s’en être fortement approchés.
Informatique quantique et chiffrement
L’un des principaux impacts attendus de l’informatique quantique porte sur les capacités de chiffrement et la sécurisation des informations. Concrètement, l’informatique quantique menace l’un des principaux systèmes de chiffrement utilisé aujourd’hui : le RSA. Nommé d’après le nom de ces créateurs – Ronald Rivest, Adi Shamir et Léonard Adleman – RSA est un algorithme de cryptographie créé en 1977 au MIT4.
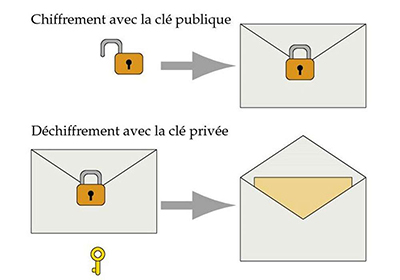
Ce chiffrement est asymétrique, ce qui signifie que la clef qui permet de chiffrer le message, la clef publique, est différente de la clef qui permet de déchiffrer le message, la clef privée. La personne qui souhaite envoyer un message récupère la clef publique du destinataire et elle encode le message avec. Puis elle envoie le message ainsi chiffré et le destinataire peut alors décrypter le message avec sa clef privé.
Afin de générer les clefs publique et privée, l’algorithme choisi deux nombres premières aléatoire P et Q, et définit N = P x Q. Puis calcule phi(N) = (P – 1)(Q – 1) et choisi aléatoirement un nombre E premier avec phi(N) et inférieur à phi(N). Enfin, il calcule D qui est l’inverse de E modulo phi(N). Alors le couple (E, N) est la clef publique et la clef privée est le nombre D.
Au plan mathématique, l’algorithme repose sur la difficulté à trouver des diviseurs entiers premiers à un nombre très grand. Dans le cas ou quelqu’un souhaiterait trouver la clef privée à partir de la clef publique, c’est ce qu’il devra faire pour dérouler l’algorithme précédent à l’envers. Même si quelqu’un arrive à avoir un calculateur suffisamment puissant réussir cette factorisation et donc briser le chiffrement, il suffira d’augmenter un tout petit peu la taille des nombres P et Q choisi au départ augmenter exponentiellement le temps de déchiffrage.
La grande fiabilité de cette méthode de chiffrage en fait la méthode de cryptage privilégiée par le grand public. La sécurité des transactions bancaires, de la majorité des sites web et des connexions à distance sont assurées en grande majorité par cet algorithme. Même les crypto-monnaies utilisent le chiffrement RSA pour s’assurer de la confidentialité des transactions. L’anonymat étant l’un des points les plus forts des crypto-monnaies, celles-ci risquent tout simplement de s’effondrer si le chiffrement RSA n’existe plus.
Cryptographie post quantique
En quoi l’informatique quantique menace-t-elle le chiffrement RSA ? Inventé en 1994 par Peter Shor, l’algorithme du même nom à pour but de se servir de la puissance des ordinateurs quantiques pour trouver les facteurs premiers d’un nombre bien plus rapidement et en utilisant bien moins de puissance de calcul qu’un ordinateur classique5. C’est à cause de cet algorithme que le chiffrement RSA est, à terme, menacé. Cependant, cet algorithme demande encore des ordinateurs quantiques puissants et, selon les estimations actuelles, le chiffrement RSA pourrait encore tenir une dizaine d’années. Pour l’exemple, actuellement aucun l’ordinateur quantique n’est assez gros pour factoriser un nombre supérieur à 15 (5×3).
Mais l’algorithme de Shor n’est pas nouveau et le monde de la cryptographie a eu le temps de se préparer. Depuis 2016, de nombreux concours sont inventés tous les ans pour créer de nouvelles manières de crypter les données qui puissent résister à l’informatique quantique, aussi bien que le RSA le fait actuellement pour les machines classiques.
Deux types de solution ont à ce jour été proposées. La première repose sur de nouveaux algorithmes de chiffrement, plus compliqués à mettre en place, plus coûteux en ressources, mais capables d’arrêter l’informatique quantique ou du moins de freiner sa capacité à déchiffrer n’importe quel mot de passe existant. La seconde option est de combattre le mal par le mal : en combinant l’informatique classique et l’informatique quantique. Bennet et Brassard ont déjà inventé, en 1984, un algorithme permettant de crypter les données de façon non seulement complètement sécurisée, mais qui, en plus d’être indéchiffrable, permet de savoir si quelqu’un essaye de vous espionner ou d’intercepter votre message6 ! Cependant, cette méthode implique que tous les systèmes de communication possèdent un ordinateur quantique, un émetteur quantique et un récepteur quantique. Donc, même si en théorie cet algorithme est parfait, il n’est pas possible à mettre en place pour le moment. Il faudra ainsi sûrement se rabattre sur la première solution le temps que des progrès techniques se fassent.
Ainsi, même si théoriquement le chiffrement RSA n’est plus fiable à 100 %, en pratique il n’est pas près de céder avant une dizaine d’années et des solutions de secours ont déjà été mises en place. L’informatique quantique n’est pas une menace pour l’instant, mais plutôt le futur des grands calculs et du cryptage.

- Jeremy Kahn, « IBM debuts quantum machine it says no standard computer can match », Fortune, 15 nov. 2021 (https://fortune.com/2021/11/15/ibm-quantum-computer-127-qubit-eagle-processor/)
- Siobhan Roberts, « This new startup has built a record-breaking 256-qubit quantum computer », MIT Technology Review, 17 nov. 2021 (https://www.technologyreview.com/2021/11/17/1040243/quantum-computer-256-bit-startup/)
- Frederic Holweck, Introduction to Quantum Algorithms
- « Wikipedia », RSA(Cryptosystem), https://en.wikipedia.org/wiki/RSA_(cryptosystem)
- « Quiskit », Learn Quantum Computation using Qiskit, https://qiskit.org/textbook/preface.html
- BB84, https://en.wikipedia.org/wiki/BB84


